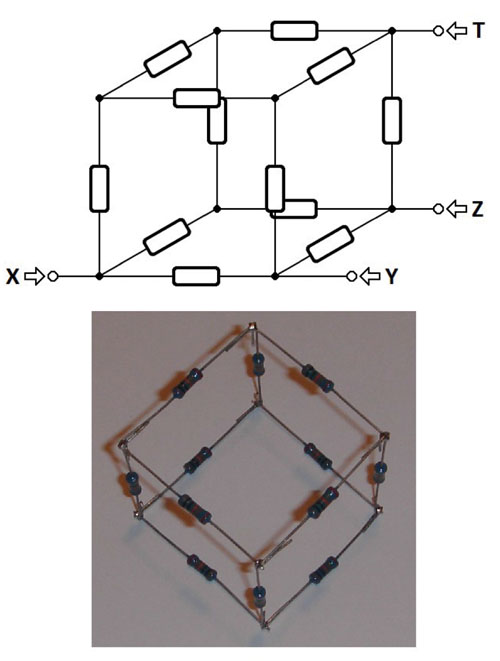
V današnjem nadaljevanju člankov s tem naslovom se bomo lotili reševanja ugank, ki sem jih zastavil v prejšnjem prispevku: kako izračunati nadomestne upornosti med točkami X in Y, X in Z ali X in T na kocki, katere robove tvorijo upori, ki imajo enako upornost R.

Model kocke, ki je prikazan na sliki 5 je izdelan z dvanajstimi upori upornosti 100 k in tolerance 1%. Uporabili ga bomo za preverjanje pravilnosti naših izračunov.
3. uganka: kakšna je nadomestna upornost med točkama X in Y kocke?
Razen tega, da kocko sestavlja večje število uporov, kot je bilo to v primeru kvadrata, v tem primeru postane bolj zapleten tudi račun, dodatno oviro pa predstavlja dejstvo, da so upori v kocki razporejeni v treh dimenzijah. Zato bomo najprej morali najti način, kako to tridimenzionalno mrežo pretvoriti v dvodimenzionalno – kar nam bo prineslo nize paralelno in serijsko povezanih uporov, s tem pa najbrž ne bi smeli imeti težav!

6[1]: Začetno stanje, računamo nadomestno upornost med točkama X in Y. Barve, s katerimi so obarvani posamezni upori so izbrane tako, da poudarijo simetrijo vezave – to nam bo znatno olajšalo izračun!
6[2]: Bodimo pozorni na rumeni upor, ki je vezan med vozlišči A in B. Če bi ga lahko vzdolžno prerezali, bi mrežo lahko razprostrli v ravnini, kot vidimo na 6[4].
6[3]: To lahko dosežemo takole! Predstavljajmo si, da rumeni upor sestavljajo štirje upori z upornostjo R, ki so med sabo povezani tako, kot je prikazano na sliki. Če je upornost vsakega od teh štirih rumenih uporov R, potem bo tudi upornost celotne takšne kombinacije enaka R (preverite!). En sam rumen upor smo torej nadomestili s skupino štirih rumenih uporov; ker se pri tem skupna upornost med vozlišči A in B ni spremenila, se tudi ni spremenila upornost celotne kocke. Tu je treba biti pozoren še na eno podrobnost: vozlišče A smo sedaj prikazali kot dve vozlišči, A in A‘, ki sta med sabo kratko povezani. Enako velja tudi za vozlišči B in B‘. Poglejmo kaj se bo zgodilo, če te kratke stike med vozlišči odstranimo!
6[4]: Če kratka stika med vozlišči A in A‘ ter B in B‘ odstranimo, lahko mrežo uporov položimo na ravnino, s čimer postane dvodimenzionalna. Ker sta spodnja in zgornja polovica mreže popolnoma enaki, bo razlika potencialov (napetost) med vozliščema A in A‘ enaka 0. Ravno to je tudi razlog, zaradi katerega smo lahko odstranili kratek stik med vozliščema A in A‘ (spomnimo se: če sta sosednji vozlišči na istem potencialu, skozi element, ki ju povezuje, ne teče nikakršen tok, zato smemo takšen element ali povezavo odstraniti). Enako velja tudi za vozlišči B in B‘.
Majhne uganke za mlade elektronike (2)
2015_SE227_55