Univerza v Ljubljani, Fakulteta za elektrotehniko
Avtor: Izr. prof. dr. Marko Jankovec
Po počitnicah na začetku novega šolskega leta učitelji ponavadi radi potipajo, če se učenci še kaj spomnijo lanske snovi preden zastavijo na novo.
In, da ne boste preveč v zadregi, naredimo na hitro ponovitev vsega, kar smo si do sedaj pogledali, za vsak do sedaj objavljeni prispevek po en najbolj pomemben stavek:
Elektromagnetna združljivost je eden od potrebnih pogojev, da lahko elektroniko prodajamo na prostem trgu kjerkoli po svetu, česar pa nepoštena poslovna praksa z daljnega vzhoda največkrat ne upošteva.
Najbolje je, da jo imamo v mislih že od začetka načrtovanja naprave, pri čemer se je potrebno držati vrste standardov, ki se ukvarjajo s prevodnimi in sevalnimi emisijami kot tudi odpornostjo naprav nanje.
Najučinkovitejše dosežemo EMC tako, da se je lotimo pri izvorih, ki so hitre spremembe napetosti in tokov v vezjih in povezavah, kjer lahko le s pravilno identifikacijo izvora težave uporabimo tudi pravo zdravilo.
Poleg izvora motnje je pomembna tudi pot širjenja motnje prek skupnih kapacitivnosti in induktivnosti, ki jih dobri načrtovalci naprav znajo identificirati v obliki prevodnih površin in tokovnih zank in zmanjšati na minimum.
Druga polovica zgodbe so sofazne motnje, na katere pri načrtovanju zaradi kompleksnejšega mehanizma dostikrat pozabimo in zato velikokrat predstavljajo trši oreh za streti.
Zanimivo a ne, da se da povzeti bistvo petih člankov v petih stavkih, kar bi nekemu mlademu in splošno iznajdljivemu študentu lahko generiral tudi GPT in bi on le ponovil naučeno na ustnem izpitu. A brez večletne prakse in poglobljenega študija bi bil kljub pozitivni šestici ravno tako neuporaben inženir kot prej. A to ne paše v ta prispevek. Gremo naprej!
Poznamo torej štiri glavne izvore elektromagnetnih motenj in sicer:
tokovno generirane diferencialne motnje, ki jih generirajo zanke s hitrimi tokovnimi spremembami
napetostno generirane diferencialne motnje, ki jih generirajo površine s hitrimi napetostnimi spremembami in se sklapljajo prek kapacitivnosti nazaj na vezje
tokovno generirane sofazne motnje, ki jih generirajo hitro spreminjajoči tokovi po masi, kar povzroča hitre napetostne razlike med različnimi točkami vezja, ki se lahko nadalje širijo v kabelske povezave
napetostno generirane sofazne motnje, ki jih generirajo hitro spreminjajoče napetosti, ki se sklapljajo prek roba tiskanine na okolico
Ko s pravilnim načrtovanjem vezja z upoštevanjem vseh v zadnjih dveh prispevkih razloženih ukrepov ob omejitvah s strani načrtovalca ohišja, konektorjev in kablov naprave do tipa in velikosti komponent, da ne govorimo o omejitvah dobavljivosti in cene, se moramo na koncu še vedno pokoriti teoriji osnov elektrotehnike. Če želimo, da naprava deluje glede na specifikacije, so napetosti in tokovi, četudi najbolj optimalni, še vedno prisotni. Torej, elektromagnetne motnje so in če so te prevelike, moramo uporabiti dodatne ukrepe, kot so oklapljanje, blokiranje in filtriranje motenj. In kar takoj so se pojavile tri ideje za tri nove prispevke. Tokrat si poglejmo tehnike filtriranja.
Filtriranje v svetu EMC je metoda, s katero želimo zmanjšati visokofrekvenčne komponente signala v nekem delu vezja, za kar se prvenstveno uporabljajo nizkofrekvenčni prepustni filtri. To lahko dosežemo z dvema mehanizmoma in sicer:
Visokofrekvenčni signal s filtrom zadržimo v čim manjšem področju vezja pri izvoru signala tako, da se ne more širiti ven in tako manj učinkovito seva v okolico. Z drugimi besedami, zmanjšamo mu velikost antene. Pri tem filter deluje kot bariera, ki odbije visokofrekvenčni signal nazaj proti izvoru.
Visokofrekvenčni signal s filtrom zadušimo tako, da njegovo energijo pretvorimo v toploto, ki nas seveda ne moti, dokler temperatura ostane znotraj varnega območja.
Ker motnje grobo ločimo na sofazne in diferencialne, poznamo tudi sofazne in diferencialne filtre. A najprej si oglejmo najosnovnejši parameter filtra, to je vstavitveno dušenje IL (ang. Insertion loss). Definirano je kot razmerje med dušenjem signala brez filtra Sbrez (ω) in dušenjem signala pri vstavljenim filtrom Sfilt (ω). Izraža se v decibelih, zato je v enačbi dodana še logaritmična pretvorba:
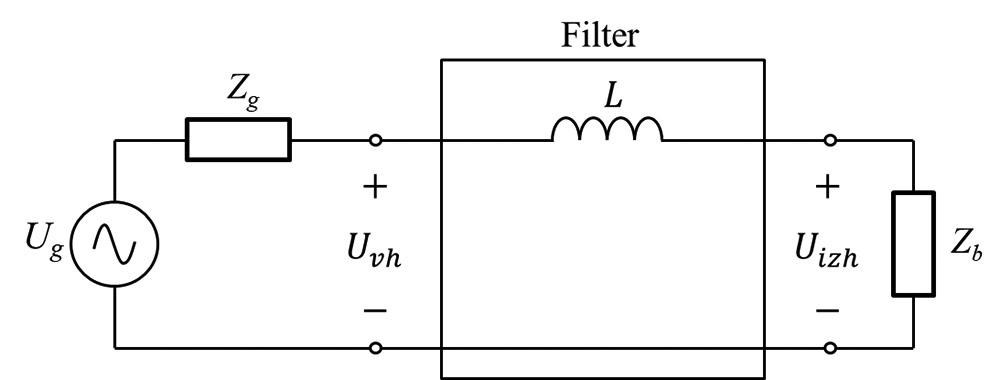
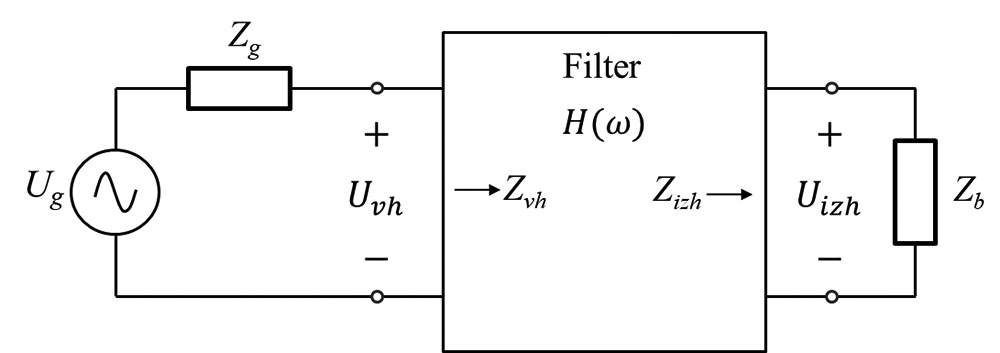
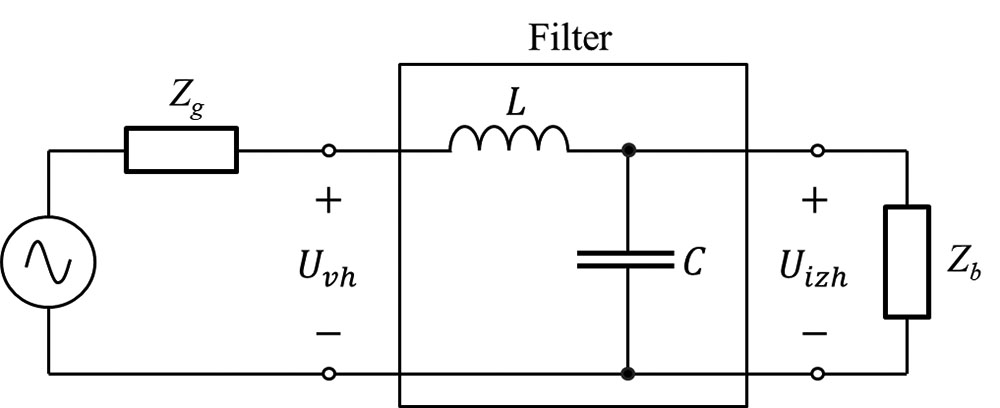
Vstavitveno dušenje IL(ω) je mera, za koliko vstavitev filtra izboljša razmere v vezju in je seveda močno frekvenčno odvisno. Odvisno pa je tudi od impedančnih razmer v vezju pred vstavitvijo filtra, zato IL(ω) nikoli ni podatek filtra samega, temveč je vedno podano glede na impedanco leve in desne strani vezja, kamor vstavimo filter. Proizvajalci filtrskih elementov zato podajajo le nekaj vrednosti IL pri par izbranih frekvencah glede na neke tipične impedance, ki se pojavljajo v najpogostejših aplikacijah. Ti podatki lahko služijo za okvirno določitev učinkovitosti dušilnega elementa v nekih razmerah. Za bolj natančno določitev je potrebno upoštevati dejanske razmere v vezju. Zato si poglejmo splošni primer na sliki 1, kjer filter kot četveropol s prevajalno funkcijo H(ω) vstavimo v vezje in s tem razdelimo vezje na dva dela. Levi del na sliki predstavlja izvor motnje Ug z nadomestno impedanco izvora Zg , medtem ko desni del predstavlja žrtev – breme z nadomestno impedanco Zb.
Za določitev vstavitvenega dušenja je potrebno najprej določiti dušenje motnje brez filtra, kar lahko ob poznanih impedancah enostavno določimo z upoštevanjem impedančnega delilnika, pri čemer je Uvh=Uizh, saj četveropola – filtra ni. Glej Formula 1.
Vidimo lahko, da bo dušenje signala generatorja veliko pri visoki impedanci generatorja Zg in nizki impedanci bremena – žrtve Zb. Ko pa vstavimo med njiju filter, le ta spremeni razmere v vezju s svojo vhodno in izhodno impedanco. In tako dobimo dva impedančna delilnika, ki določita vhodno napetost filtra Uvh in prek prevajalne funkcije filtra H(ω) tudi izhodno napetost Uizh, ki je napetost na bremenu – žrtvi Zb.
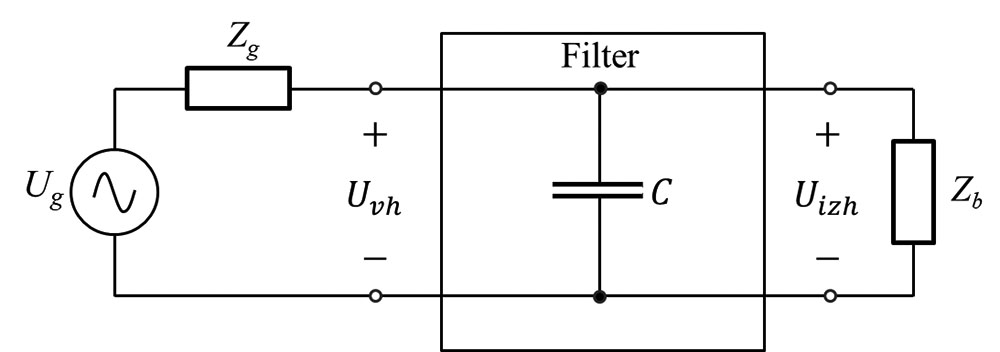
Poglejmo si en primer najenostavnejšega filtra, ki ga sestavlja zgolj en kondenzator C. Ta je vezan vzporedno z impedanco bremena – žrtve Zb, ki v kombinaciji z impedanco izvora Zg predstavlja nizkofrekvenčno-prepustni filter. Vsakemu študent prvega letnika, ki je poslušal Osnove elektrotehnike II je hitro jasno, da je dušenje novega vezja lahko izračuna kot, glej Formula 2.
Če izraz vstavimo v osnovno enačbo za dobimo vstavitveno dušenje kondenzatorja, glej Formula 3.
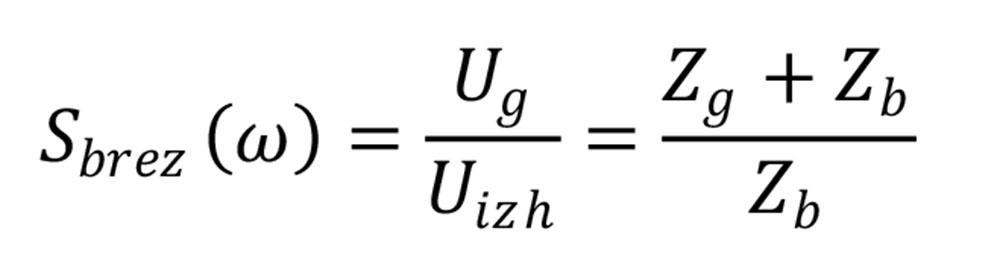
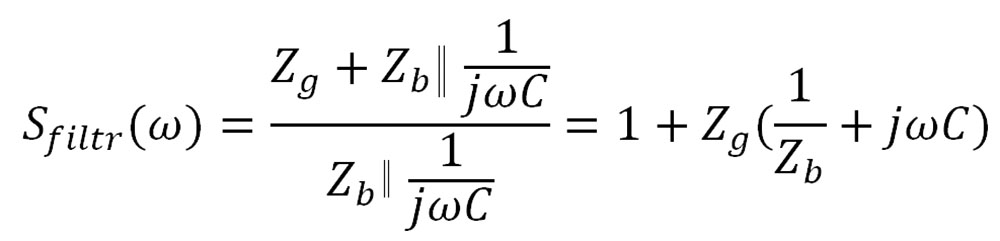
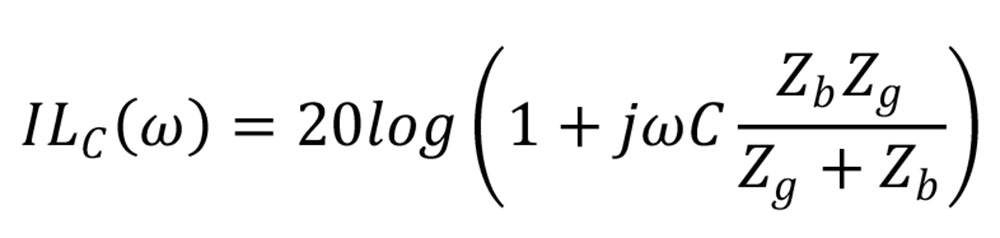
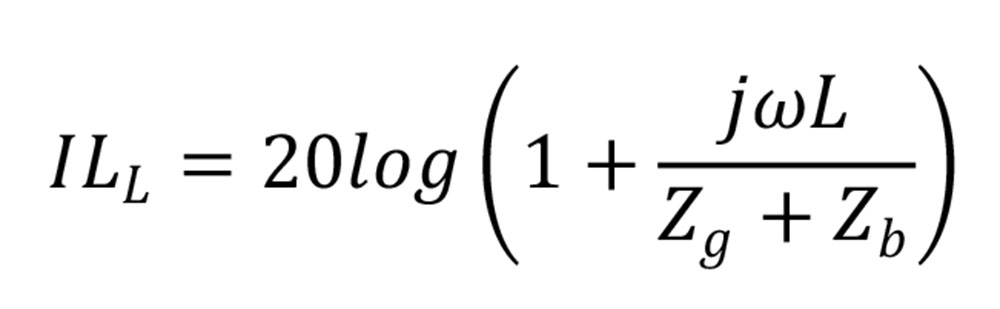
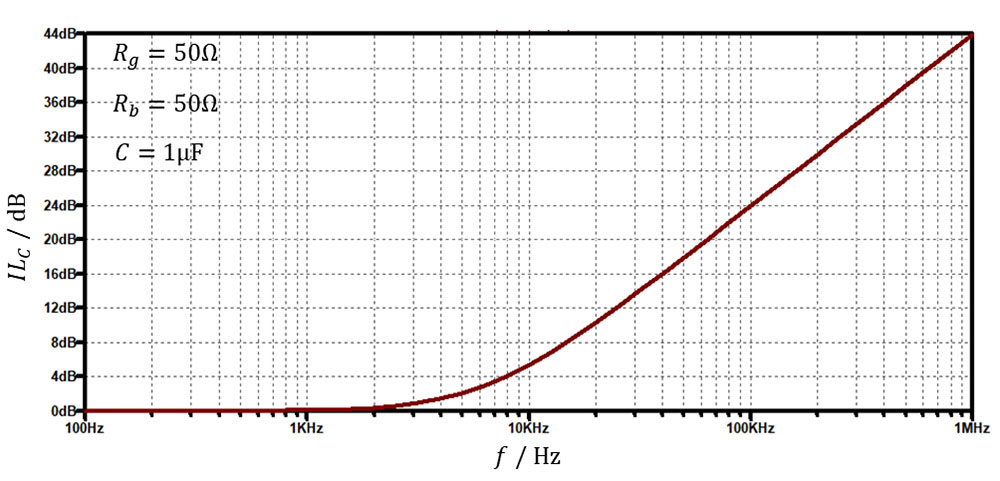
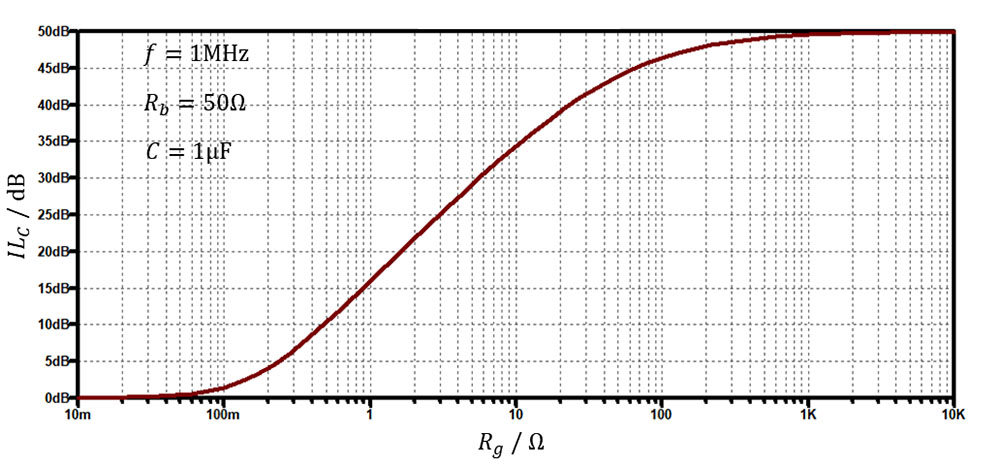
Hitro lahko vidimo, da je vstavitveno dušenje poleg impedance kondenzatorja ZC=1/jωC odvisno tudi od obeh okoliških impedanc. Če zaradi enostavnosti privzamemo, da sta impedanci realni (Zg=Rg in Zb=Rb), ILC seveda narašča s frekvenco s strmino 20 dB/dekado v področju, kjer je celoten izraz v oklepaju veliko večji od 1. To je za primer kondenzatorja s kapacitivnostjo 1μF v standardnem 50 ohmskem sistemu (Rg=Rb=50Ω)kar kaže slika 3. A četudi se nahajamo v frekvenčnem območju, kjer bi pričakovali visoko vstavitveno dušenje ILC, to velja le, kadar je Rg ≫ Rb. V nasprotnem primeru, ko je Rg ≪ Rb, je vstavitveno dušenje lahko tudi zanemarljivo majhno in se približa 0 dB, kar lepo prikazuje slika 4. Če poenostavimo: lahko se vam zgodi, da vstavitev kondenzatorja ne bo imela nobenega učinka.
Kaj pa, če namesto kondenzatorja vstavimo tuljavo? Da bi dosegli funkcionalnost nizkofrekvenčnega prepustnega filtra, jo moramo povezati zaporedno, kot kaže slika 5.
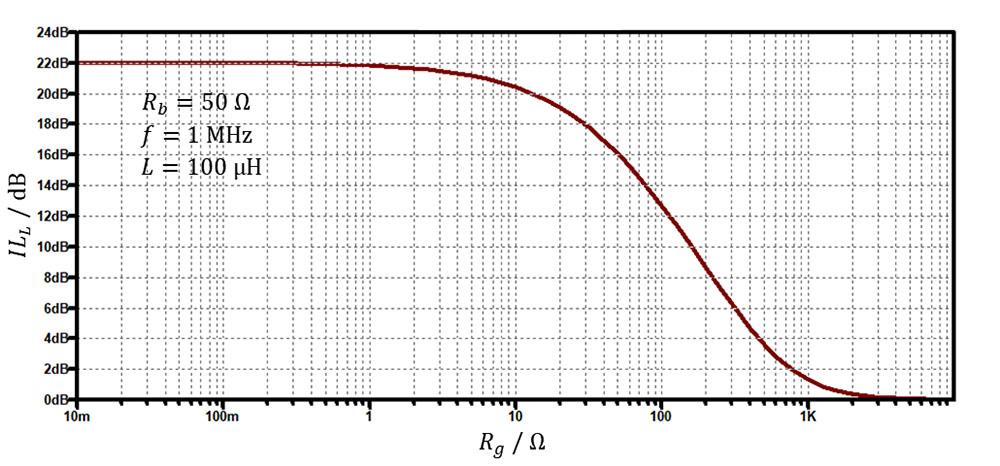
S tako vezavo dobimo podoben potek vstavitvenega dušenja ILL, kot s kondenzatorjem, kar je razvidno tudi iz enačbe, ki si jo lahko podobno kot v primeru kondenzatorja, izpeljete sami, glej Formulo 4.
Ko pogledamo odvisnost ILL od impedance (upornosti) izvora motnje Rg, je potek obraten kot pri kondenzatorju. Vstavitveno dušenje je veliko, če velja ωL ≫ Zg+Zb, kar se ponavadi zgodi z višanjem frekvence. A tudi pri visokih frekvencah je lahko ILL minimalno, če sta ena ali obe impedanci visoki. To se iz slike 6 lepo vidi, ko ILL pade proti 0 dB, ko povečujemo serijsko upornost vira motnje Rg.
Kaj se lahko naučimo iz teh dveh primerov? Obe osnovni izvedbi filtrov uporabljata v teoriji brezizgubne elemente. To pomeni, da delujeta na principu odboja energije proti izvoru motnje saj motnje ne moreta pretvoriti v toploto. Iz teorije o maksimalnem prenosu moči s filtrskim elementom skušamo slediti najslabšemu prenosu motnje iz izvora proti bremenu – žrtvi v želenem frekvenčnem področju s tem, da iščemo impedančno neprilagoditev. To pa dosežemo takrat, ko v frekvenčnem področju motnje izberemo glede na impedanco vira in bremena – žrtve najbolj neusklajeno impedanco filtrskega elementa. Ker se najbolj neugodne motnje običajno pojavljajo pri višjih frekvencah, tam obravnavamo kondenzator kot nizko-impedančen, tuljavo pa kot visoko-impedančen element. Zato v primeru nizke impedance (upornosti) vira motnje uporabimo tuljavo, v primeru visoke pa kondenzator, kar lepo kažeta sliki 4 in 6.
Zaključimo za prispevek z LC filtrom, ki je osnovna kombinacija obeh filtrskih elementov, prikazan na sliki 7.
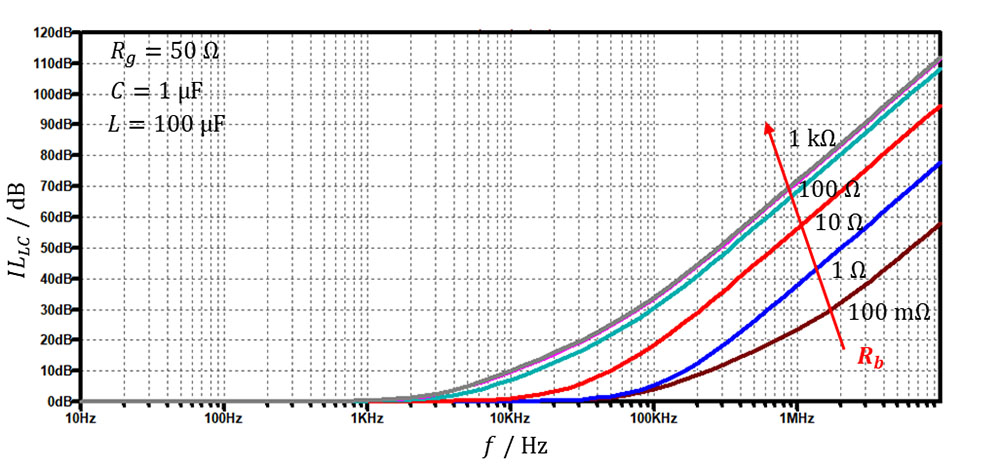
Tak filter daje dvakratno strmino poteka vstavitvenega dušenje glede na posamezen element, ki raste kar s 40 dB/dekado, kot kaže slika 8 za klasični 50 ohmski sistem.
Prikazano je tudi, kako se pri visokih frekvencah, kjer filter deluje, vstavitveno dušenje filtra z večanjem bremenske upornosti Rb močno povečuje, saj je na izhodu filtra kondenzator z nizko impedanco v tem frekvenčnem področju.
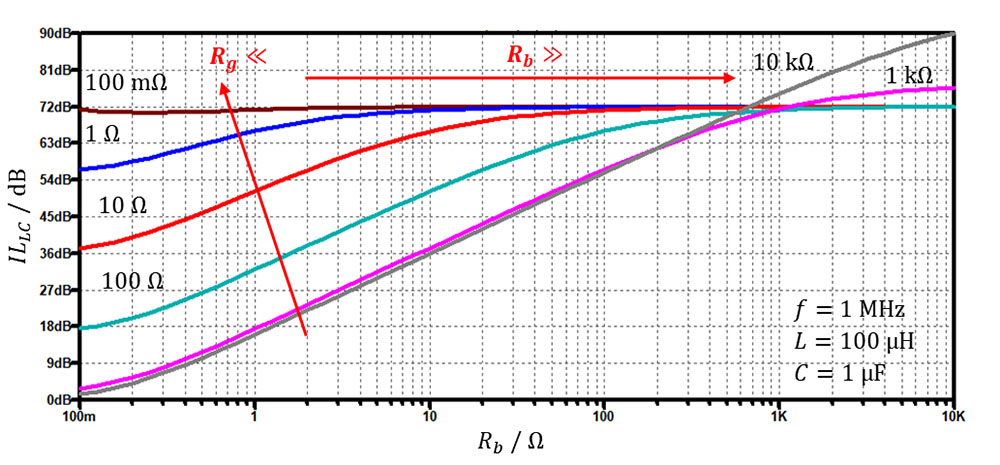
Pri katerih impedancah vira in bremena je ta LC filter torej najbolj učinkovit? Če sledimo receptu o neprilagojenosti, potem je največja ILLC v primeru, ko imamo nizko impedanco vira motnje Rg (visoka vhodna impedanca tuljave) in visoko impedanco bremena – žrtve Rb (nizka izhodna impedanca kondenzatorja), kar lepo prikazuje slika 9.
Opazimo pa lahko tudi, da pri visokih vrednostih Rb dobimo pri visokih Rg še boljši rezultat. Vzrok je v tem, da ima tuljava pri frekvenci 1 MHz impedanco enako 628 Ω, kar pomeni, da se pri upornostih vira nad 1 kΩ spet pojavi vhodna neprilagojenost. To seveda velja le za to frekvenčno območje, pri višjih frekvencah pa se tudi ta meja dvigne.
Tokrat smo bili malo daljši, a upam, da tudi dovolj praktični in lahko tole sago o filtrih zaključimo z enim lepim sistematičnim prikazom osnovnih pravil izbire ustreznega filtra, ki se glasi takole:
Za ustrezno izbiro filtra moramo poznati impedance vezja v frekvenčnem področji, ki ga želimo filtrirati.
Kondenzator ima pri visokih frekvencah nizko impedanco, tuljava visoko.
Če je impedanca izvora motnje visoka, začnemo s kondenzatorjem, sicer s tuljavo.
Če je impedanca bremena – žrtve nizka, končamo filter s tuljavo, sicer s kondenzatorjem.
Toliko o pravilu na palec glede izbora filtrov, s pomočjo katerega se odločimo za enega izmed naslednjih osnovnih tipov filtrov: L, C, LC, CL, LCL in CLC. Če bi bil svet tako enostaven, bi zgoraj napisano zapečatilo vse debele knjige in simulacijske programe za vedno. A žal je realnost še mnogo kompleksnejša. Še dobro, kajti kdo bi sicer potreboval inženirje elektrotehnike, če bi bilo vse tako enostavno? A o tem in še več v naslednjih prispevkih, ki sledijo.
