Univerza v Ljubljani, Fakulteta za elektrotehniko
Avtor: Izr. prof. dr. Marko Jankovec
Epošta: marko.jankovec@fe.uni-lj.si
V prejšnjem prispevku smo si pogledali model EMC in s tem v zvezi načine generiranja in brezžičnega prenosa motenj. Ločili smo bližnje in daljne polje in smo oboroženi s teorijo elektromagnetike v stilu indukcijskega (»pun intended«) sklepanja Sherlocka Holmesa rešili dva zagonetna primera prenosa motnje.
Elektromagnetne motnje pa se ne širijo brezžično, temveč tudi po žicah. Takim motnjam rečemo prevodne (konduktivne) motnje. Najlaže si jih predstavljamo kot napetostne motnje, ki je nastanejo zaradi tokov, ki tečejo po skupnih impedancah povezav. Dva tipična primera ponazarja slika 1. Levo se agresor (tokovni vir) in žrtev napajata z istega napajanja prek skupne napajalne povezave. Tok agresorja se prenaša na žrtev preko padca napetosti na impedanci povezave. Primer takega prenosa motnje bi bil recimo primer stikalnega napajalnika s slabim vhodnim filtrom (agresor), ki generira prevodne motnje, ki se širijo preko skupne impedance 230V omrežja na radijski sprejemnik (žrtev). Desni primer pa prikazuje, kako se šum agresorja prenaša na žrtev prek skupne povezavo na maso. V praksi tak primer srečamo na vezju, kjer ima digitalni del vezja (agresor) skupno maso z analognim (žrtev) in se tako prenaša motnja.
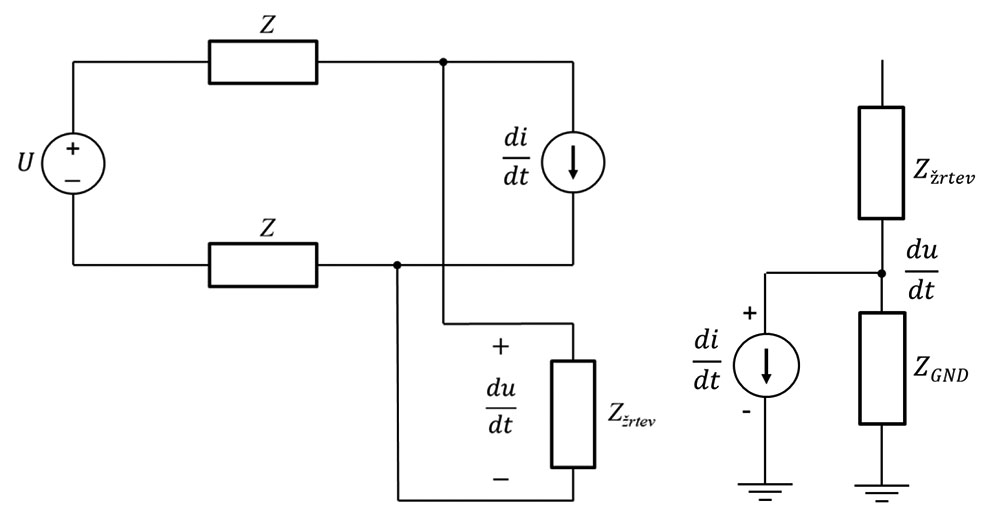
Sedaj pa si bomo kot pravi elektroniki, pogledali dogajanje v vezjih, pri čemer seveda ne bomo pozabili uporabiti osnov elektrotehnike.
Vsako elektronsko vezje lahko topološko opišemo z vozlišči in zankami. Vozlišča električno opišemo z njihovo napetostjo in zanke s tokovi, kot določata oba Kirchoffova zakona. V prejšnjem članku smo spoznali, da so viri sevanja:
hitre spremembe napetosti vozlišč, ki se kapacitivno sklapljajo v okolico in
hitre spremembe tokov zank, ki se induktivno sklapljajo v okolico.
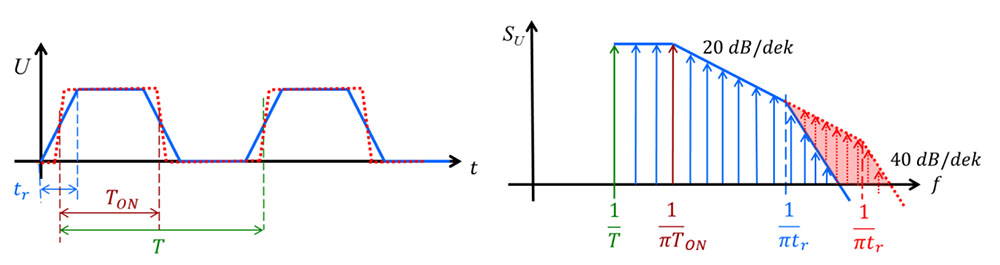
Dajmo se najprej vprašati, kje srečamo hitre spremembe napetosti in tokov in kako jih opišemo? Najlaže to storimo v svetu digitalnih vezjih, kjer vladajo signali, ki prehajajo bolj ali manj hitro med dvema diskretnima napetostnima nivojema, ki določata logično ničlo in enico. Za analizo jih lahko poenostavljeno opišemo z trapezodno obliko, ki vsebuje tri parametre: periodo T, trajanje logične enice TON in dvižni čas oz. čas upadanja (tr oz. tf), kot prikazuje slika 2.
Taki signali so zelo frekvenčno bogati, zato jih vedno uvršamo med potencialne izvore motenj. Njihov frekvenčni spektra ima dve značilni mejni frekvenci. Prvo določa čas TONdrugo pa dvižni čas tr. Iz stališča EMC najbolj prispeva visokofrekvenčni del signala, katerega obseg določa dvižni čas tr, kot je prikazano na sliki 2 desno. Če dvižni čas skrajšamo (rdeče črtkana črta na sliki 2 levo), se visokofrekvenčni del spektra razširi (rdeče polje na sliki 2 desno). Zato za omejevanje sevanja stremimo k čim počasnejšim spremembam signala (zniževanje du/dt in di/dt), kar omejuje frekvenčno bogatost signalov in s tem zniževanje problemov zaradi sevanja. Izkaže se, da je to pomembnejši faktor kot sama frekvenca signala, če prav sta oba parametra med seboj povezana. Visokofrekvenčnega signala pač ne moremo izvesti s poljubno nizkim časom prehoda, medtem ko je obratno povsem možno. Frekvenca signala je pogojena s želeno hitrostjo prenosa informacije in te za neko aplikacijo ne moremo zniževati. Lahko pa si izberemo najdaljši možni čas prehoda, ki še ustreza osnovni frekvenci signala. To možnosti ponuja tudi vedno več mikrokrmilnikov, kjer si lahko izbiramo med več hitrostmi splošnih vhodno/izhodnih priključkov in tako vplivamo na EMC končnega vezja.
Sedaj ko poznamo lastnosti vira (napetostnega ali tokovnega) signala se lahko lotimo naslednje pomembne komponente, ki prispeva k izdatnosti sevanja. Če se vrnemo na članek v prejšnji številki revije, je pri napetostno generiranih motnjah to medsebojna kapacitivnost, pri tokovnih pa medsebojna induktivnost. Medsebojna pa zato, ker povezujeta vir motnje – agresorja s sprejemnikov – žrtvijo. Oboje lahko sicer znižamo že s tem, da povečamo razdaljo med njima. To seveda ni praktično, pri meritvah EMC pa so razdalje merilne antene od naprave celo določene v standardu in zato na to nimamo vpliva.
Zniževanje možnosti razširjanja motenj moramo torej izvesti z pravilnim načrtovanjem vezja in naprave. Eno od izkustvenih pravil (na palec) je, da je minimalna dolžina linije, ki že deluje kot antena enaka dvajsetini valovne dolžine F1:
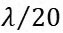
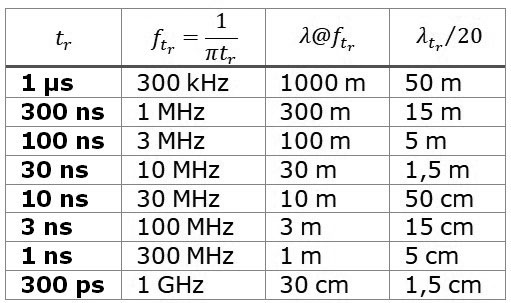
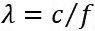
V zraku velja F2: , in če izračunamo valovno dolžino signala pri mejni frekvenci spektra, določeni z dvižnim časom, potem dobimo naslednjo tabelo, tabela 1:
Pri načrtovanju povezav hitrih signalov se skušamo držati pravila, da naj bodo linije, ki vsebujejo hitre signale, čim krajše. A vrednosti v zgornji tabeli so zgolj okvirne in še zdaleč ne predpisujejo strogih omejitev. Pri načrtovanju vezij se najprej ukvarjamo z generacijo signalov v bližnjem polju, kjer znižujemo oba glavna mehanizma širjenja motenj, to so medsebojne kapacitivnosti in induktivnosti. Medsebojne kapacitivnosti znižujemo s tem, da minimiziramo površine vozlišč, ki vsebuje hitre napetostne spremembe in jih obdamo z vseh strani s čim večjo površino mase. Na ta način zaključimo električno polje nazaj proti izvoru. Za zmanjšanje magnetnih motenj pa na medsebojne induktivnosti vplivamo z minimizacijo površin zank, po katerih tečejo visokofrekvenčni tokovi.
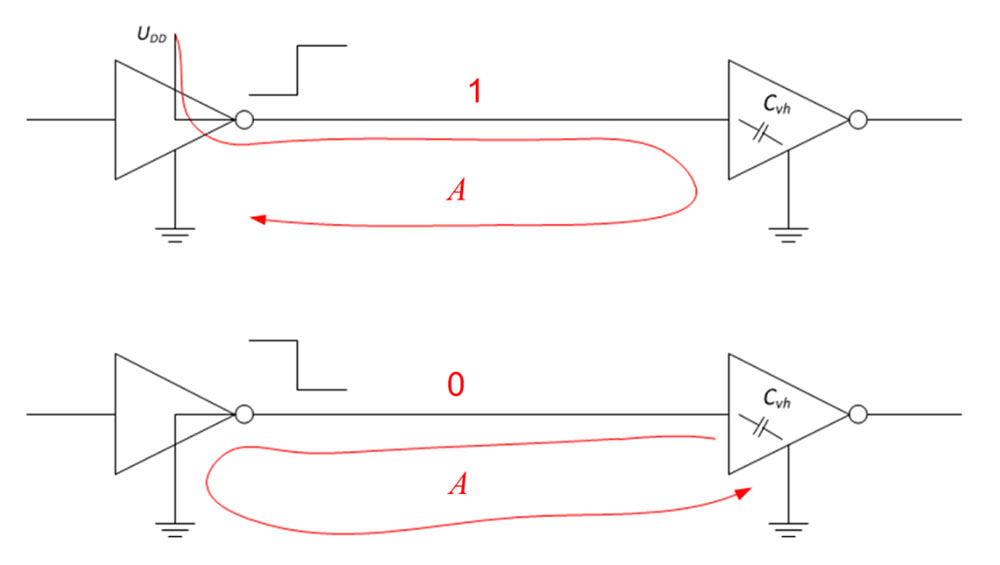
Poglejmo si digitalno povezavo med izvorom na levi in ponorom na desni, kot jo prikazuje slika 3. Če želimo na linijo postaviti logično enico, visok potencial na liniji dosežemo tako, da v izvoru priklopimo linijo prek notranjega MOS tranzistorja na napajalno napetost. Pri tem steče električni tok, ki napolni vhodno kapacitivnost ponora na desni strani. Ta tok steče po masi nazaj vse do napajalnega vezja, kot veleva tokovni Kirchoffov zakon. Če pa želimo postaviti na linijo logično ničlo, potem moramo skleniti linijo na izvoru signala na maso, pri čemer se kondenzator na ponoru izprazni in tok spet steče po masi, a tokrat proti ponoru.
Obakrat imamo hitro spremembo napetosti na liniji in hitro spremembo toka v zanki, s površino A, kot je označeno na sliki 3.
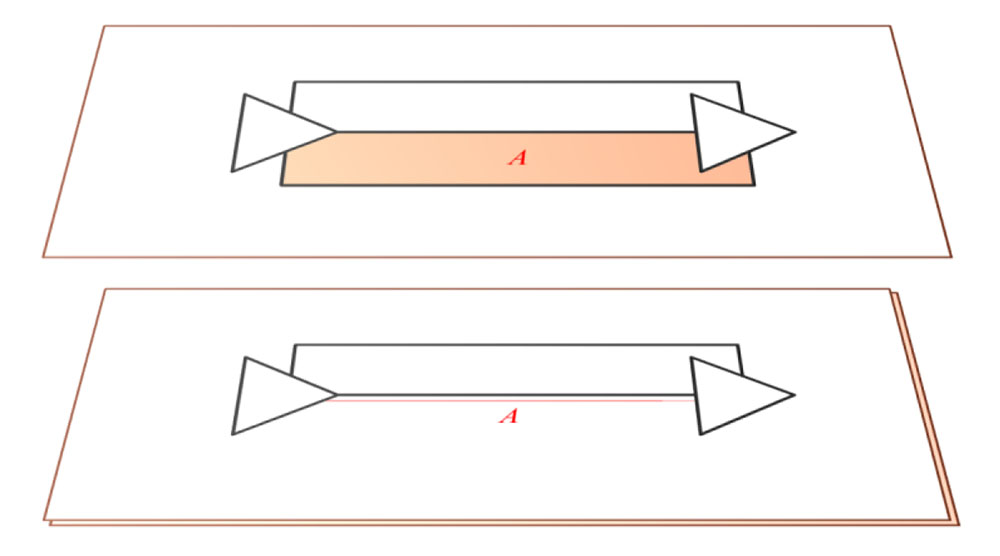
S tem problemom se v digitalnih vezjih uspešno spopadamo z tehniko povezovanja neprekinjene mase pod hitrimi povezavami z uporabno večplastnih vezij, kot je prikazano na sliki 4. Že pri dvoplastnem vezju je možno v nekaterih primerih z optimalnimi pogoji povezati neprekinjeno maso pod hitro linijo, kot se vidi na sliki 4. Pri večplastnih vezjih pa je to še bolj enostavno, kjer si lahko za maso privoščimo tudi več kot le eno plast.
Na ta način ubijemo dve muhi na en mah: zmanjšamo površino zanke, kjer tečejo visokofrekvenčni tokovi in zagotovimo veliko masno površino v bližini linije, kjer so hitre spremembe napetosti. Masne površine pod linijami so ugodne še iz mnogo drugih razlogov, ki jih bomo mogoče odkrili kasneje.
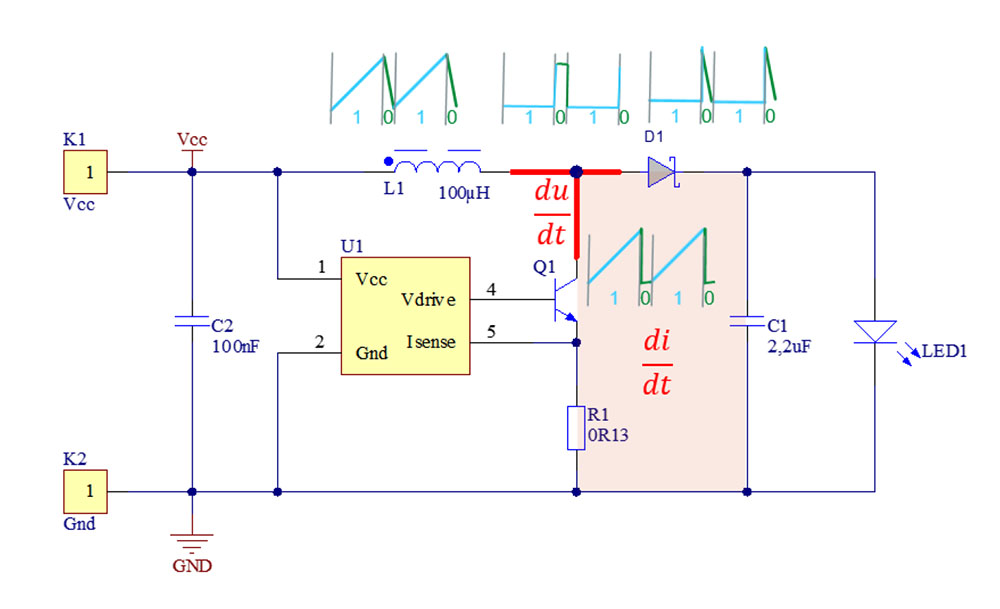
Poglejmo si še en bolj zanimiv primer, ki pa prihaja iz analognega sveta, kjer pa ravno tako obstajajo hitri prehodni pojavi napetosti in tokov – stikalni pretvornik. Slika 5 prikazuje shemo stikalnega pretvornika navzgor (boost converter) za napajanje svetleče diode (LED). Tokovne oblike vej so narisane z modro in zeleno barvo, ki označujejo poteke tokov, ko tranzistor prevaja (1) in ko ne prevaja (0). Vidimo, da je strmina toka skozi tuljavo v obeh stanjih tranzistorja omejena in določena z induktivnostjo tuljave po enačbi F3, kar pomeni, da je tokovna zanka, ki vključuje tuljavo s stališča motenj v osnovi ni kritična. Medtem, ko tokova skozi preklopna elementa, kot sta dioda in tranzistor vsebujeta hitre vklope in izklope tokov, kot je razvidno iz slike spodaj tvorita kritično tokovno zanko, ki jo je potrebno zmanjšati. Kaj pa hitre napetostne spremembe? Te so najbolj očitne na t.i. stikalnem vozlišču, ki je na shemi označeno z rdečo, kajti tam se napetost ob preklapljanju tranzistorja zelo hitro spreminja iz skoraj nič na maksimalno. Površino tega vozlišča moramo zmanjšati na minimalno in zagotoviti okrog njega maso.
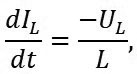
Poglejmo sedaj dve rešitvi načrta tiskanega vezja, levo slaba in desno boljša. Boljša izvedba ima zmanjšano stikalno vozlišče du/dt in minimalno površino tokovne zanke di/dt. Dodatni površini mase na obeh straneh sta povezani na maso in tako omogočata najkrajše tokovne poti po masi kot tudi učinkoviti kapacitivni sklop za napetostno generirane motnje.
Zaključek
Optimalno načrtovanje tiskanega vezja zahteva predvsem temeljito analizo sheme za poglobljeno poznavanje delovanja vezja, identifikacija kritičnih tokovnih zank in napetostnih vozlišč in posledično minimizacija obeh. Vezja seveda ne moremo v celoti minimizirati na neskončno majhno piko in če brez premisleka skušamo minimizirati vse, pri tem sprejmemo preveč kompromisov, ki težko pripeljejo do optimalnega rezultata. Recept za dober rezultat je v tem, da najprej optimalno povežemo kritične dele vezja, nato pa še ostalo. In tu brez znanja osnov elektrotehnike, kot ste verjetno opazili tudi sami, pač ne gre.
