Načrtovalci analognih vezij se pri napovedovanju delovanja vezij močno opirajo na simulacije. Vrednost simulatorja je odvisna od tega, kako dobro lahko napoveduje fizično realnost in kako hitro lahko pride do rezultatov. Neskladje med simuliranim in realnim delovanjem lahko povzroči drage iteracije v postopku razhroščevanja izdelka.
Orodje SPICE se uporablja za simuliranje analognih vezij, saj lahko izračuna celotno obnašanje poljubnih vezij za velike signale. Za uspeh orodja SPICE na področju simulacij analognih vezij so zaslužne tri numerične metode. Natančneje:
- Newtonova metoda za iskanje rešitev v vezjih z nelinearnimi elementi.
- Metode z razpršenimi matrikami, ki ogromne matrike zapakirajo v naslovni prostor uporabnega računalnika.
- Implicitno integriranje za integriranje diferencialnih enačb, ki izhajajo iz reaktanc vezij.
- Sposobnost določenega simulatorja SPICE, da zanesljivo zagotovi pravilne rezultate, je odvisna od tega, kako dobro so izvedene te metode. Ta članek opisuje, zakaj je orodje LTspice boljše pri zagotavljanju pravilnih rezultatov od drugih izvedb orodja SPICE.
Newtonova metoda
Newtonova metoda pomeni razčlenitev karakteristike I-V za vsako nelinearno napravo v vezju v Taylorjevo zaporedje, pri katerem se nato ohranita le prva dva člena in se reši tako pridobljeni sistem linearnih enačb. Če je rešitev sistema linearnih enačb dejansko točka, v kateri smo razčlenili Taylorjevo zaporedje, je rešitev tega sistema dejansko pravilna rešitev prvotnega nelinearnega vezja, ker je Taylorjev približek v tej točki točen, v njeni bližini pa dober približek1. Uspešna konvergenca Newtonove metode pomeni iskanje numeričnega dokaza, da je bila najdena pravilna rešitev za vaše vezje.
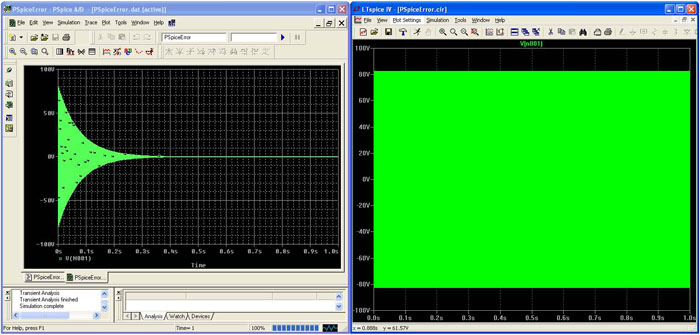
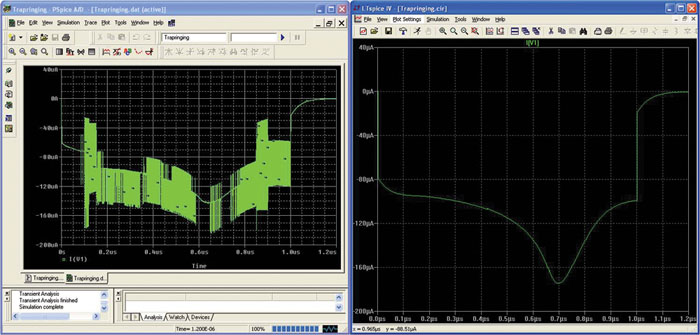
Robustnost Newtonove metode je odvisna od (1) zveznosti po vrednosti in naklonu za vse karakteristike I-V za elemente v vezju in (2) obvoda vseh nelinearnih elementov s kapacitivnostjo, da je rešitev iz prejšnjega časovnega koraka dobra izhodiščna točka za Newtonovo metodo v trenutnem časovnem koraku. Pogoja (1) in (2) sta izpolnjena v vsakem fizičnem vezju, vendar pa programi SPICE tega ponavadi ne obravnavajo pravilno, saj imajo polprevodniške naprave v izvedbi Berkeley SPICE nezveznosti in so se te napake pri izvedbi prenesle v plačljive izvedbe orodij SPICE. Te nezveznosti se ne pojavljajo v izvedbi LTspice. Za primer glejte sliko 1, ki kaže karakteristiko diode v izvedbah PSpice2 in LTspice. Seznam vej v obeh primerih je:
* Nezveznost karakteristike I-V pri diodi v izvedbi PSpice
V1 N001 0 0
D1 N001 0 D
.dc V1 -.3 -.2 2u
.probe
.model D D(Is=10n)
.end
Karakteristika I-V za diodo v izvedbi PSpice je nezvezna po vrednosti in naklonu. Take nezveznosti se pojavljajo v večini polprevodniških naprav v izvedbi PSpice in v nobeni v izvedbi LTspice.
Metode za razpršene matrike
Taylorjevo zaporedje je večdimenzionalno – po ena dimenzija za vsako neznano napetostno vozlišče v vezju. Za analogno integrirano vezje lahko to pomeni 100.000 različnih napetostnih vozlišč, kar pomeni matriko prevodnosti velikosti 100.000 x 100.000, kar bi pri koeficientih matrike z dvojno natančnostjo zahtevalo 80 milijard bajtov. Za dostop do toliko pomnilnika nimajo dovolj naslovnih linij niti najsodobnejši 64-bitni procesorji. Na srečo so skoraj vsi koeficienti nič, tako da jih ni treba shranjevati. Metode z razpršenimi matrikami beležijo le neničelne elemente. To dopušča reševanje ogromne matrike v dokaj majhnem naslovnem prostoru.
Razpršenost matrike izhaja iz fizikalne narave praktično uporabnih vezij. Večina vozlišč je povezanih z le nekaj drugimi vozlišči. Če na primer izpiše te matriko prevodnosti za vezje, ki je videti kot mreža iz uporov, je matrika skoraj diagonalna, saj je vsako vozlišče uporovno povezano le s sosednjimi vozlišči. Praktično uporabna vezja imajo še manj povezav kot mreže. Razpršenost matrike pri velikih analognih vezjih je reda milijoninke. Ta razpršenost je tisto, kar dopušča reševanje matrike s sodobnimi računalniki. Newtonova metoda za analogna vezja ni izvedljiva brez metod za razpršene matrike.
Razlike med izvedbami orodja SPICE
Linear Technology
2016_SE238_14
