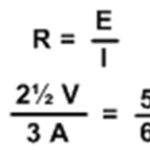Drage bralke in dragi bralci, občasno v revijo Svet elektronike objavimo tudi članek, ki je primeren za elektronike začetnike. Pričujoči članek morda ni namenjem resničnim začetnikom, je pa dobre primer, kako uporabljati intuicijo in logiko.
RF CAFE
Dvanajst žic z upornostjo R je povezanih v kocko. Kolikšna je ekvivalentna upornost med diagonalnima koncema kocke? Problem bomo rešili na dva načina.
Ta vsebina je samo za naročnike
1. način:
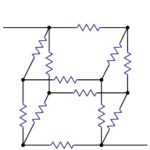
Na sliki vidite strukturo kocke, ki je sestavljena iz 12 uporov. Upori so električno povezani med 8 vrhovi. Vsak upor ima vrednost 1 Ω, vendar lahko uporabimo katero koli vrednost, če so vsi enaki.
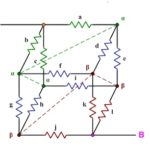
Tu pride do izraza intuicija. Barvno označevanje se uporablja za lažje sledenje uporom in povezanim vozliščem (spodaj). Zaradi simetrije je potencial (napetost) na treh vozliščih z oznako “α” enak. Ker med vozlišči s potencialno razliko 0 V ne teče tok, jih lahko med seboj kratkostično povežemo, ne da bi to vplivalo na celovitost vezja. Enako lahko storimo za vozlišča z oznako “β”.
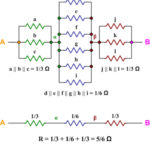
Ko ste povezali med sabo ta vozlišča, dobite ekvivalentno vezje, ki je prikazano spodaj. Kot lahko vidite, sta dva sklopa treh vzporednih uporov v zaporedju z enim sklopom šestih vzporednih uporov. Tako imamo 1/3 Ω v seriji z 1/6 Ω v seriji z 1/3 Ω, kar je enako 5/6 Ω.
Zdaj bomo predstavili še en način reševanja problema kocke upora. Struktura je ponovljena tudi tukaj.
2. način:
Pri analizi je bistven Kirchhoffov tokovni zakon, ki pravi, da je vsota tokov, ki vstopajo v vozlišče in izstopajo iz njega, enaka nič.
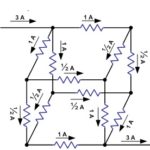
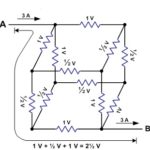
Prvi korak je ugotovitev, da se v vozlišču z enakimi upori tok, ki vstopa v vozlišče, enakomerno porazdeli med število izhodnih vej – v tem primeru med tri. Zaradi priročnosti sem v vogalu z oznako “A” pripisal vhodni tok 3 ampere, tako da bo skozi vsako izhodno vejo tekel 1 amper. Upoštevajte, da skozi vsako vejo teče 1 A.
Na drugi strani vsake od teh vej je še eno vozlišče z dvema izhodnima vejama. Zaradi simetrije se vhodni tok ponovno enakomerno razdeli, tako da v vsako vejo teče ½ A. Če pogledamo izhodno vozlišče kocke z oznako “B”, ugotovimo, da gre za enako situacijo kot pri vozlišču “A”.
Za trenutek seštejte tokove v in iz vsakega vozlišča in preverite, ali se vsi seštevajo, kot je potrebno.
Zdaj, ko poznate tok skozi vsako vejo in veste, da ima vsaka veja po en upor vrednosti 1 Ω, lahko po Ohmovem zakonu izračunate napetost na vsakem uporu.
Naslednji korak je seštevanje napetosti od vhodnega vozlišča “A” do izhodnega vozlišča “B”. Vsaka pot, ki jo izberete, potuje po treh robovih in vse skupaj znašajo 2 ½ volta.
Na koncu uporabite Ohmov zakon, ki pravi, da je upornost enaka napetosti, deljeni s tokom. Tako kot pri drugi metodi analize je dobljena ekvivalentna upornost 5/6 Ω.
Zaključek
Za vajo spajkanja lahko sestavite takšno kocko z enakimi upori in preverite, ali izračunana upornost drži. Pri sestavljeni kocki lahko merite tudi napetosti med posameznimi vozlišči in se prepričate, kako drži razlaga v tem članku. Predvsem pa bo sestava takšne kocke res dobra vaja za spajkanje, saj se je za lepo oblikovano kocko potrebno potruditi!