Avtor: dr. Simon Vavpotič
Avtor: dr. Simon Vavpotič
2019_270_44
Brez digitalnega procesiranja signalov ni hitrih brezžičnih komunikacij in visoke ločljivosti videa in zvoka. Zanimalo nas je, kako izdelati programsko orodje za PC ali PIC32 za hitro analizo z A/D pretvornikom vzorčenih signalov.
Čeprav imamo velikokrat občutek, da je domači PC namenjen predvsem preprostemu pisarniškemu delu in popoldanskim zabavnim aktivnostim, med katerimi zagotovo ne manjka računalniških iger, je z ustreznim programskim orodjem v veliko pomoč tudi pri digitalni analizi signalov, na osnovi katere lahko preverimo modele za digitalno obdelavo signalnih tokov in jih kasneje prenesemo v vgrajeno programsko opremo mikrokontrolerjev. Digitalni analizator lahko uporabimo tudi pri diagnostiki napak v elektronskih vezjih.
Ta vsebina je samo za naročnike
A/D pretvorba
Predpogoj za digitalno analizo realnih signalov je njihov prenos iz analognega v digitalni svet. Pri tem nujno potrebujemo ustrezen A/D pretvornik. Enostavni 10-bitni in 12-bitni A/D pretvorniki, ki zmorejo vzorčiti signale s frekvencami tja do 1 MHz, so že standardno vgrajeni v številne mikrokontrolerje – tudi v PIC32. Kadar želimo zmogljivejše vzorčenje, moramo uporabiti zunanji A/D pretvornik. V seriji treh člankov z naslovom A/D pretvorniki z visoko ločljivostjo v SE266, SE267 in SE268 smo zgradili lastno vezje za 32-bitno vzorčenje počasnih analognih signalov. Po drugi strani, v internetu najdemo tudi rešitve za kakovostno vzorčenje visoko frekvenčnih signalov. Zahtevnejši lahko v ta namen uporabijo tudi digitalni osciloskop, če le ta omogoča tudi zajemanje izmerjenih vrednosti v obliki nepretrganega toka podatkov.
Zakaj digitalna obdelava signalov?
A/D pretvorba je le prvi korak, s katerim signale iz analognega sveta prenesemo v digitalni svet, kjer se lotimo njihove analize z eksaktnimi matematičnimi orodji, pri čemer so rezultati obdelav ob razpoložljivosti dovolj velike procesne moči, dovolj velikega pomnilnika in ustreznega algoritma odvisni predvsem od kakovosti zajema podatkov.
Glavni procesor PC-ja je neprimerno zmogljivejši od vsakega mikrokontrolerja. Zato ga lahko s pridom uporabimo za preverjanje pravilnosti algoritmov in za najbolj zahtevne obdelave podatkov. Medtem, ko mikrokontroler uporabimo za izvajanje namenskih optimiziranih obdelav signalov. Denimo, če želimo izdelati digitalni procesor zvoka, ki deluje kot izenačevalnik zvoka, in hkrati po protokolu I2S posreduje podatke digitalnemu avdio ojačevalniku, lahko matematični model za procesiranje zvoka najprej preizkusimo v PC-ju in ga nato prepišemo v vgrajeno programsko kodo za PIC32. Tako, osebni računalnik, denimo pri nastavljanju barve zvoka, ne bo več potreben.
V digitalnem spektralnem analizatorju z analizo frekvenčnega spektra in časovno analizo poiščemo signale opazovanih naprav, pri čemer nas pogosto zanima njihova pojavnost in moč, vsekakor pa tudi pomeni pojavnosti njihovih kombinacij. V tem pogledu je zanimiva, na primer analiza v sobi odbitega ultrazvočnega signala, na osnovi katere lahko izmerimo razdalje od ultrazvočnega oddajnika do sten in drugih predmetov. Že izdelana tovrstna tipala že omogočajo enostavne meritve, za kompleksnejše meritve, pri katerih želimo natančno analizirati signal iz ultrazvočnega mikrofona pa moramo izvesti s pomočjo natančne analize digitaliziranega odbitega ultrazvočnega signala.
Podobno je tudi z uporabo tipal za zaznavanje prisotnosti v prostoru. Preprosta tipala, ki temeljijo večinoma na analognih vezjih, zaznavajo le prisotnost ali odsotnost gibanja, medtem ko lahko z vzorčenjem in podrobnejšimi digitalnimi analizami izvemo bistveno več podatkov, kot sta približna oddaljenost in velikost predmeta, kar omogoča dinamično nastavljanje praga zaznavanja gibanja. Denimo, pri alarmnih sistemi si prav gotovo ne želimo, da bi jih sprožila že večja žuželka, ki se je po naključju ujela v stanovanju.
Časovni in frekvenčni prostor
Z A/D pretvornikom signal zajamemo kot časovno zaporedje numeričnih vrednosti (npr. v digitalni obliki zapisanih realnih števil), pri čemer je od frekvence vzorčenja odvisna najvišja frekvenca signala, ki ga bomo še lahko obdelali. Nato lahko enostavne analize, kot so: izračun efektivne vrednosti izmeničnega signala, meritev časa vzpona ali upada signalnega impulza, ali preučevanje zaporedja komunikacijskih znakov, izvajamo v časovnem prostoru. Ko smo že omenili komunikacijske znake, povejmo, da sta v digitalnem svetu v osnovi le dva, 0 in 1, vendar lahko D/A pretvornikom kombinacije več bitov predstavimo v obliki različnih vrednosti napetosti – komunikacijskih znakov, ki jih nato z A/D pretvornikom v sprejemniki pretvorimo nazaj v zaporedja bitnih vrednosti, ki ustrezajo posameznimi komunikacijskim znakom. Zato je komunikacijskih znakov pri sodobnih digitalnih komunikacijah več. Hkrati so glede na izbrano vrsto modulacije lahko opisani tudi z drugimi fizikalnimi veličinami, kot sta faza in frekvenca. Pri kompleksnejših analizah signalov se zato vsekakor ne moremo izogniti tudi njihovi pretvorbi v frekvenčni prostor (npr. s pomočjo Fourierove transformacije).
V frekvenčnem prostoru lahko opazujemo zaporedje jakosti sinusnih signalov preko frekvenčnega celotnega spektra v merilnem dosegu. Predstavljamo si, da infrardečo sprejemno diodo (ali tranzistor) povežemo z virom napajanja in A/D pretvornikom, nakar želimo poiskati nosilno frekvenco izbranega daljinskega upravljalnika. Zato daljinski upravljalnik močno približamo sprejemni diodi, med pritiskom na tipko posnamemo signal iz sprejemne diode z A/D pretvornikom in ga s Fourierovo transformacijo pretvorimo v frekvenčni prostor. Vendar so v tem signalu zajeti tudi drugi svetlobni signali, predvsem vidna svetloba, ki jih ne potrebujemo, vendar vseeno lahko poiščemo frekvenco z najvišjo jakostjo signala, ki prestavlja izbrani daljinski upravljalnik. Naslednji korak je iskanje podatkovne vsebine, oziroma ugotavljanje katero tipko smo pritisnili. Tu si moramo pomagati s časovno analizo.
Način delovanja daljinskega upravljalnika lahko v digitalni logiki izvedemo demodulacijo, s pomočjo katere ponovno pridobimo digitalni tok podatkov, s katerim je podana koda posamezne tipke. Od tu naprej lahko uporabljamo analizo v časovnem prostoru. Programirljivi nadomestni daljinski upravljalniki omogočajo zajem signala za določene tipke originalnega daljinskega upravljalnika in njegovo shranjevanje v pomnilnik v digitalni obliki. Je pa res, da se sicer redko zgodi, da signala kake tipke ne uspejo pravilo posneti, oziroma reproducirati. Tu bi si lahko pomagamo z analizatorjem signalov, s katerim natančno pregledamo posredovan tok podatkov, ki ga izluščimo s pomočjo poprejšnje analize v frekvenčnem prostoru. Nato lahko izdelamo kakovostnejše vezje za reprodukcijo signalov.
Kombinirana analiza signalov
Analize v časovnem prostoru se pogosto lotevamo po izvedbi analize v frekvenčnem prostoru, saj želimo z analizo v frekvenčnem prostoru razločiti informacijske znake in nato s časovni analizo razumeti njihovo zaporedje, da bi lahko razbrali vsebino posameznega sporočila.
Predstavljajmo si otroško igračo na daljinsko upravljanje preko radijskih signalov, za katero želimo izdelati nadomestni daljinski upravljalnik. Najprej s spektralno analizo v frekvenčnem prostoru poiščemo nosilni signal, nato izdelamo digitalni filter, s katerim izločimo na nosilno frekvenco vpet moduliran signal, v katerem nato poiščemo komunikacijske znake, ki so navadno izredno preprosti (naprej, nazaj, levo, desno).
Pri izvajanju kompleksnejših analiz potrebujemo več načrtovanja. Vendar je prednost analize digitaliziranih signalov predvsem ta, da jo lahko izvedemo tako, da sestavimo različne matematične funkcije, ki opravljajo ekvivalentne operacije kot bi jih analogna vezja, ki predstavljajo različne dele sprejemnikov signalov. Z uporabo matematičnih funkcij dosežemo izjemno visoko natančnost, ki je pogojena predvsem z zmogljivostjo (signalnega) procesorja. V našem primeru vlogo slednjega začasno prevzame kar centralna procesna enota PC-ja. Šele, ko program optimiziramo, ga prenesemo v vgrajeno programsko opremo mikrokontrolerja. Za bolj zahtevne aplikacije lahko uporabimo tudi namenske digitalne procesorje signalov z namenskimi funkcijskimi enotami, s katerimi poenostavljajo določene operacije.
Programsko orodje: Fourierova transformacija
Ko se praktično lotimo pisanja programa za analizo digitaliziranih signalov, moramo med drugim misliti tudi na dovolj veliko hitrost obdelave podatkov, kar navadno dosežemo z izbiro višjega programskega jezika, ki nudi ustrezne optimizirane funkcijske knjižnice in pa zna enostavne računske operacije prevesti v hitro izvedljivo strojno kodo procesorja. Pogosto smo primorani uporabiti programski jezik C ali C++, ki hkrati omogočata natančno delo s pomnilnikom, v katerem poteka obdelava digitaliziranih signalov. Če nimamo na voljo vseh matematičnih knjižnic, denimo tiste za izvedbo Fourierove transformacije, jih brez večjih poiščemo v Internetu. Vendar moramo paziti, da jih v lastnem programskem orodju tudi pravilno uporabimo.
Denimo, Fourierova transformacija pretvori digitaliziran signal v frekvenčni prostor kot zaporedje kompleksnih vrednosti, mi pa želimo, na primer, le spektrogram efektivnih vrednosti napetosti po frekvenčnem obsegu. V takem primeru nas zanimajo le realne komponente kompleksnih vrednost, medtem ko lahko fazne zamike razberemo iz imaginarnega dela kompleksnih vrednosti.
Vsekakor je pomembna tudi predpriprava podatkov za algoritem, ki izvaja Fourierovo transformacijo. Običajna implementacija algoritma za hitro Fourierovo transformacijo (FFT) izvede transformacijo kar v istem pomnilniku, v katerega smo prenesli zaporedje analognih vrednosti. Vendar iz A/D pretvornika zajamemo zaporedje realnih vrednosti, ki jih lahko spremenimo v kompleksne vrednosti tako, da vsako dodamo še imaginarno komponento z vrednostjo 0. A zdaj se upravičeno sprašujemo, kako naj to naredimo. Večina algoritmov za izvajanje FFT pričakuje zapis kompleksnih vrednosti na način, da je najprej zapisana realna komponenta, na to pa še imaginarna, nakar je na enak način zapisna naslednja kompleksna vrednost. Na to je dobro misliti že ob zajemu podatkov iz A/D pretvornika, pri katerem lahko v pomnilnik namesto realnih zapisujemo kompleksne vrednosti, sestavljene iz realne vrednosti in ničelne imaginarne komponent. Tako kasnejše preoblikovanje podatkov z vrivanjem ničel pred izvedbo FFT ne bo potrebno.
Programsko orodje: Grafični prikaz signala
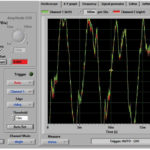
Računalniška grafika navadno ne predstavlja posebnih težav za implementacijo v osebnih računalnikih, medtem ko je v mikrokontrolerjih ne potrebujemo, razen pri gradnji priročne merilne naprave. Pri izrisu signala na zaslon želimo pogosto posnemati funkcionalnosti digitalnih osciloskopov, pri čemer ne moremo brez številčne skale, ki natančno prikazuje izmerjene vrednosti napetosti v časovnem ali v frekvenčnem prostoru. Pomembno je tudi, da natančno umerimo A/D pretvornik in da hkrati natančno poznamo hitrost vzorčenja. Tako bomo lahko v diagramih pravilno umerili prikaz časa in frekvence.
A/D pretvorniki imajo za prilagajanje, umerjanje in kalibriranje navadno vgrajene posebne funkcionalnosti, kot so: frekvenca vzorčenja, število hkrati zajemanih analognih kanalov, boljši pa tudi možnost nastavljanja predojačenja vhodnega signala.
Izbira merskega intervala na časovni osi je odvisna predvsem od izbrane frekvence vzorčenja in velikosti grafičnega okna, v katerega želimo diagram narisati. Vendar bomo morali največ truda vložiti v pravilen prikaz vrednosti napetosti, saj moramo iz nastavitev A/D pretvornika in dejanske vrednosti napetosti njegovega vira referenčne napetosti najprej izračunati območje merjenja in šele nato lahko za vsako izmerjeno digitalno vrednost natančno ugotovimo kateri napetosti ustreza.
Na tak način si lahko vzorčeni digitalni signal s končnim trajanjem ogledujemo podobno kot avdio posnetke, za primeren osciloskopski način prikaza v realnem času pa se moramo navadno nekoliko bolj potruditi. Če želimo posnemati najbolj starinske osciloskope brez proženja signala, lahko digitalne vrednosti iz izravnalnika enostavno izrisujemo na zaslon brez sinhronizacije, a potem je malo verjetno, da bo na primer sinusni signal, miroval. Proženje prikaza izmeničnega signala sicer brez težav vežemo na spremembo predznaka digitaliziranih vrednosti in/ali na določen minimalni nivo napetosti s preprosti pogojnim stavkom (IF) v programski kodi. Po drugi strani, si pri neperiodičnih signalih končne dolžine, denimo tistih iz daljinskega upravljalnika, bolj pomagamo z njihovim statičnim ogledom v obliki avdio posnetka.
Omenimo še to, da lahko za prikaz vrednosti napetosti signala namesto linearne vgradimo tudi logaritemsko skalo. Vendar gre tu zgolj za preračun izmerjenih vrednosti s pomočjo logaritemske funkcije, medtem ko se prikaz časovne skale ne spremeni. Med zelo atraktivne možnosti sodi tudi prikaz vrednosti amplitude napetosti in relativnega časa meritve posameznega vzorca, ki sestavlja diagram. Prikaz se sproži ob preletu računalniške miške.
Programsko orodje: Frekvenčni in slapovni diagram
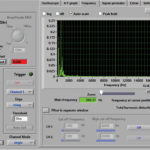
Prikaz signala po pretvorbi v frekvenčni prostor se od prikaza v časovnem prostoru razlikuje po tem, da so na ordinatni osi (os X) namesto referenčnih vrednosti časa referenčne vrednosti frekvenc. Pogosto se odločimo za logaritemski prikaz, s katerim natančneje zajamemo nizke frekvence, višje pa prikažemo bolj zgoščeno. Po drugi strani, se lahko tudi pri napetostih odločimo za logaritemski prikaz vrednosti, še posebej če uporabljamo A/D pretvornik z ločljivostjo 16 bitov ali več.
Klub temu nam pri prikazu frekvenčnega spektra pogosto manjka časovna komponenta, ki omogoča spremljanje njegovega spreminjanja skozi čas. Tu si lahko pomagamo s trirazsežnimi grafi, vendar se zaradi zahtevnosti njihovega izrisa in manjše preglednosti pogosto raje odločamo za slapovne diagrame, katerih jakost napetosti po določenih frekvenčnih območjih prikažemo s pomočjo barvne lestvice, denimo tako, da pomenijo »hladnejše« barve (kot so modri odtenki) nižje vrednosti, »toplejše« barve (npr. rdeči in rumeni odtenki) pa višje vrednosti. S tem lahko v eno vrstico barvnega zaslona (oziroma horizontalno) izrišemo celoten frekvenčni spekter v določenem trenutku, v naslednjem trenutku pa v novo vrstico izrišemo nov prikaz frekvenčnega spektra. Tako nastane trak, ki se spušča od vrha proti dnu zaslona. Ko pridemo do dna, vse vrstice pomaknemo za eno navzgor, da lahko izrišemo naslednjo vrstico, pri čemer najvišja vrstica izgine. Če omogočimo shranjevanje slapovnega diagrama, se lahko kasneje z drsniki ob robu grafičnega okna pomaknemo navzgor do začetka izrisa.
Slapovni diagram je odlično orodje za iskanje signalov preko celotnega frekvenčnega spektra, ki ga lahko zajamemo z A/D pretvornikom. Ko iskani signal odkrijemo, lahko del frekvenčnega spektra, kjer se pojavlja, natančneje obdelamo, oziroma približamo in tako morebiti odkrijemo tudi dodatne nosilne frekvence, oziroma vrsto uporabljene modulacije. Vsekakor je pri ročnem delu s pomočjo slapovnega diagrama nemogoče odkriti vseh podrobnosti, zato potrebujemo avtomatizacijo obdelave signalov.
Programsko orodje: Samodejna analiza signalov
Iskanje in analizo signalov v frekvenčnem spektru lahko izvajamo tudi s pomočjo avtomatiziranih programskih orodij. Denimo, če iščemo pojavnost signala, ki ga oddaja določen signalni vir, lahko iskanje samodejno uskladimo z začetkom oddajanja tega vira. S tovrstno avtomatizacijo si lahko, denimo pomagamo pri analizi delovanja daljinskih upravljalnikov. Če ne vemo, na kateri frekvenci oddajajo, lahko najprej shranimo časovno zaporedje spektrov v času neoddajanja in nato še eno zaporedje v času oddajanja. Nato z računalniškim algoritmom izvedemo primerjavo obeh slapovnih diagramov, oziroma obeh zajetih zaporedij slik frekvenčnega spektra po času. S pomočjo statistične obdelave lahko dokaj enostavno poišče razlike, ki nastanejo med oddajanjem daljinskega upravljalnika in tako poišče nosilno frekvenco. Naslednji koraki so omenjeno odkrivanju načina modulacije in vsebine prenosa podatkov.
Prav vsak korak analize časovnega diagrama frekvenčnega spektra je mogoče avtomatizirati. Hkrati se lahko po ugotovitvi nosilne frekvence dokaj enostavno osredotočimo samo na izdelavo digitalnega demodulatorja in analizo toka podatkov, s katerim je moduliran nosilni signal.
Med metode za samodejno analizo signalov lahko vključimo celo metode umetne inteligence, s katerimi lahko odkrivanje določenih vrst signalov vežemo tudi na različne baze znanja, ali pa omogočimo analizatorju učenje tipičnih značilnosti določenih vrst signalov. Pri slednjem lahko s pridom uporabimo celo nekatere nevronske mreže, denimo Kohonenovo, ki delujejo kot samodejni klasifikatorji, ali pa nevronske mreže s povratnim prevajanjem signalov, ki se lahko naučijo značilnih vzorcev v časovnih zaporedjih in jih nato uporabimo pri sprotnem iskanju takih vzorcev v sklopu digitalne analize signalov.
Digitalno procesiranje signalov v mikrokontrolerju
Čeprav je zmogljivost mikrokontrolerja navadno precej omejena, lahko vanj vgradimo od enostavnih pa tudi do dokaj kompleksnih algoritmov, s katerimi lahko izvajamo analize zaporedij digitalni zaporedij in podatke pripravimo za nadaljnjo obdelavo v PC-ju (denimo Fourierovo transformacijo), ali pa z metodami analitičnimi metodami in umetne inteligence iščemo želene podatke, kot sta nosilna frekvenca in faza nosilnega signala iz najbližje naprave.
Vsekakor lahko zmogljivost mikrokontrolerja s pridom uporabimo za pripravo podatkov v tako obliki, ki jo najlažje obdelamo v PC-ju. Pri tem lahko mikrokontrolerju naložimo le toliko nalog, da obenem nemoteno izvaja osnovna opravila, kot vzorčenje analognih signalov ter predpriprava in prenos podatkov v PC.
Pri avtonomnih sistemih z zahtevnimi obdelavami podatkov, denimo inteligentnem robotskem krmilniku, je smiselno izvajati tudi namenske kompleksnejše analize podatkov, oziroma zaporedij digitalnih vrednosti s tipal. Vendar pri tem ni potrebno izvajati prenosa podatkov izven mikrokontrolerja. Obenem je izbira vrste obdelava podatkov odvisna tudi od potreb, ki se pojavljajo pri potovanju robota po prostoru. Denimo, ko robot s kamero zazna predmet, vanj usmeri signal merilnika razdalje (ultrazvočnega, radarskega) in nato meri in analizira odziv. Če je potrebno, lahko med izvajanjem analize stoji in se začne premikati šele, ko na podlagi analize podatkov sprejme odločitev o načinu in smeri nadaljnjega gibanja.
Programske knjižnice
Pri programiranju PIC32 skoraj ne moremo mimo obsežne programske knjižnice Math Library v Microchip Harmony z bogato funkcionalnostjo, ki podpira funkcije za digitalno procesiranje signalov (DSP). V projekt jo vključimo s pomočjo Harmony Configuratorja. Vsekakor je vključeno računanje FFT, kakor tudi izračunavanje filtrov z neskončnim odzivom (IIR). Po drugi strani, lahko izdelamo samostojno napravo z lastnim grafičnim prikazovalnikom s pomočjo knjižnice Graphic Stack in/ali knjižnice tretjih proizvajalcev.
Sicer je v spletu veliko (plačljivih in zastonjskih) splošnih matematičnih knjižnic za numerično obdelavo digitaliziranih signalov, predvsem za programski jezik C, v katerih najdemo različne implementacije funkcij za digitalno analizo in procesiranje signalov. Uporabimo jih lahko tako v sklopu Microchipovih programskih razvojnih okolij, kot v sklopu razvojnih okolij za PC, med katerimi je eno najbolj popularnih Microsoft Visual Studio.
Med njimi je že tretja različica Numerical Recipes (http://numerical.recipes), ki je stara, a zelo uporabna plačljiva programska knjižnica (stane 49 USD). Naročnikom je na voljo za programska jezika C in C++. Vsi algoritmi so tudi v obliki izvorne kode, uporabne za gradnjo lastne programske knjižnice, ki jo lahko vgradimo v program za PC, PIC32, ali kak drug računalnik ali mikrokontroler.
Omenimo še zadnjo različico knjižnice FFTW (3.3.8) (http://www.fftw.org), ki je jo dobimo v oblikah za uporabo na PC z vektorskimi procesorskimi ukazi SSE/SSE2/Altivec in napravah s procesorji ARM Neon. Aplikacijski vmesnik je prirejen za v programske jezike C in Fortran.
Naslednjič
Spoznali smo osnovne principe digitalne obdelave signalov v mikrokontrolerju ali PC-ju. Prihodnjič se bomo podrobneje lotili razvoja programske opreme za analizo digitalnih signalov za PC in PIC32 in med drugim spoznali tudi različne implementacije FFT ter Lagrangeovih digitalnih filtrov. Vsekakor ne bo poudarek na matematičnih opisih, temveč na oblikovanju praktičnih programskih rešitev in povezovanju različnih programskih knjižnic, ki jih potrebujemo pri gradnji kompleksnejših algoritmov. Pri tem se bomo lotili tudi mogočih napak in pasti, v katere se lahko zapletemo, če se napačno lotimo praktične implementacije.