Če naše aplikacije zahtevajo odčitavanje analognih napetosti, je logična izbira mikrokontroler, ki je poleg branja sposoben podatke tudi matematično obdelati. Atmelovi 8-bitni AVR mikrokontrolerji so dovolj zmogljivi, da lahko te podatke hitro obdelajo, Bascom programski jezik s svojimi matematičnimi funkcijami poenostavlja sicer zahtevne operacije, vgrajena periferija pa omogoča več, kot si upamo pričakovati od AD pretvornika. Običajno branje napetosti na posameznih vhodih in osnove vzorčenja smo si bolj podrobno ogledali v Elektroniki za začetnike, “Programiranje VI”, tokrat pa bomo podrobneje spoznali diferencialno merjenje napetosti.
Diferencialno merjenje napetosti
Med glavnimi lastnostmi posameznega mikrokontrolerja (slika 1) včasih zasledimo tudi število diferencialnih kanalov, s katerimi lahko priključene napetosti merimo diferencialno.
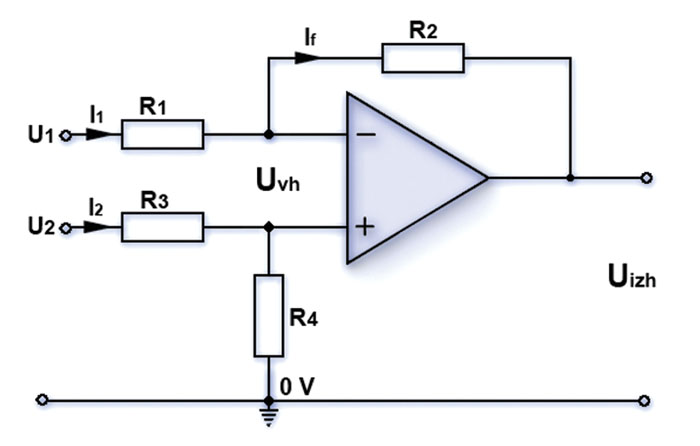
In kaj naj bi to pomenilo? Merimo lahko razliko napetosti na analognih vhodih, dveh priključkih mikrokontrolerja, prebrani rezultat pa predstavlja razliko med njima. Delovanje je podobno kot pri operacijskih ojačevalnikih z diskretnimi elementi v vezavi ojačevalnika razlike napetosti – kar je čisto pravi analogni diferencialni ojačevalnik (slika 2).
Analogni diferencialni ojačevalnik
Da malo osvežimo spomin, kako takšna merjenja izvajamo v analognem svetu in pokažemo na podobnost z delovanjem periferije za diferencialno merjenje napetosti v mikrokontrolerju, bomo na kratko opisali vezavo in delovanje operacijskega ojačevalnika, če ga priključimo tako, da deluje kot diferencialni ojačevalnik.
Kadar nas bolj kot resnična vrednost neke napetosti včasih zanima razlika napetosti v primerjavi z neko znano (referenčno) napetostjo, je to veliko bolj primeren način, sploh v primerih, ko sta razliki med napetostmi zelo majhni. Poleg tega smo lahko pri tem nekoliko zviti in samo to razliko ojačimo za nek znan faktor. Kasneje bomo z odčitavanjem te (ojačene) vrednosti natančno vedeli, kakšna je razlika med neznano napetostjo in tisto, katere vrednost poznamo.
V osnovi velja za izračun enačba s slike 3, vendar v praksi vezje poenostavimo tako, da izberemo enaki upornosti za upora R1 in R3, ter enaki vrednosti za R2 in R4. S takšnimi vrednostmi se nam formula poenostavi in na koncu dobimo zelo preprosto formulo, ki jo vidimo na sliki 4.
Iz enačbe vidimo, da nam razmerje med R2(R4) in R1(R3) neposredno pomeni faktor ojačenja diferencialnega ojačevalnika, v oklepaju pa vidimo, da se nahaja razlika napetosti na obeh vhodih. Razliko napetosti bomo torej ojačili z nekim faktorjem ojačenja. Iz enačbe lahko tudi razberemo, da bo ojačenje = 1, kadar bosta vrednosti upornosti R1 in R2 enaki. V tem primeru bomo na izhodu operacijskega ojačevalnika dobili le vrednost napetosti, ki je enaka razliki napetosti na vhodih.
Elektronika za začetnike – Programiranje mikrokontrolerjev X (34)
2012_SE201_45
